弦振動
|
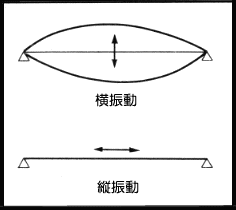
弦の振動には、弦の張られた方向に垂直に振動する横振動と、
弦の方向に振動する縦振動が考えられる。右図→
横振動は、弦の質量と張力により生じ、縦振動は弦自体が伸び縮みするもので、 弦の素材に関係する。実際に弦を弾くと、この両者が組合わされた弦を生じる。 しかし縦振動の成分は非常にわずかであり、横振動の方が重要な役割を果している。 そこで弦振動に関しては横振動のみを扱うものとし、 弦振動とは横振動のことを意味しているものとする。 さらに弦の材質は全体が均一で、張力も一定であり、 弦自身は完全に柔軟性を有するものとする。 以上のような仮定に基づくと、弦振動を表わす運動方程式は 数学的に編微分方程式の境界位置問題の形をとる。 簡単に説明すると、弦は連続体でありそれぞれの部分が、 位置と時間に依存して運動を行ない、それらが、弦の境界即ち、 固定点の条件によって決定されるということである。 |
 |
 |
弦は連続体であり、単一共振系のように書き表す訳にはいかない。
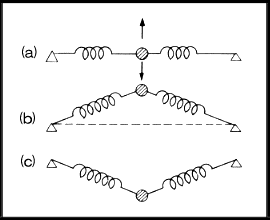
いま両端が固定された弦を下図←の(a)のように、
一つの集中質量の両端がバネを介して止められているとすると、
その質量の振動は単一共振系と同じで、現われる共振動数はただ一つである。 即ち質量を持ち上げて離すと一つの規則的な振動を行い、 その振動数は次のように与えられる。
|
|
πは円周率でありπ≒3.14である。
弦を等価的に下図↑の(a)のように表わすと右の式→の振動数で振動するのであるが、
これは実際に弦に現われる振動数と異なる。 長さLで両端が固定された均一な弦では、弦の単位長の重さを綿密度と言いσとすると、 ↓下のような振動数を有する。 |
|
|
↑上の２つの式を違いをみるためにm=Lσであることに注意すると、
一番上の式↑は左←のような式に書き換える事ができる。 Tは弦の張力である。 |
|
このように弦を単一共振動系に置き換えても、正しい解を求め得ない。
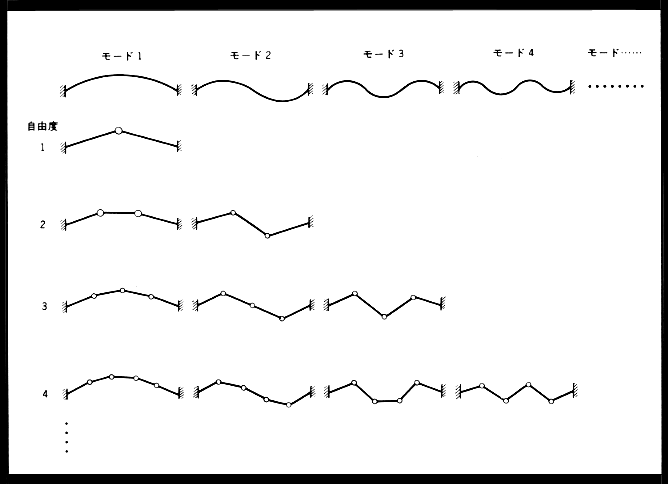
それでは弦の質量を分け、質点の数を増やしてゆくとどうなるであろうか。
下の図↓では弦は前述のように柔軟性を有しているものとしている。
その結果、色々な振動が可能である。このような種々の振動成分をモードと読んでいる。
ここで
の意味を簡単に述べると次のようになる。 即ち、弦が長ければ長いほどその振動数は低く、弦の質量は重いほど低い。 さらに張力が強ければそれだけ振動数は高くなる。 結局ギターの6弦は1弦より重く、それだけ低い音を発生する事ができる。 |
|
n = 1,2,3,･･･ |
最も低い振動数を与えるのは第一次モード。
または基本モードと呼ばれ、
その振動数は
のとおりである。
第２、３、･･･次の高次モードの振動数は→の式の整数倍である。
即ち、弦のすべての基準振動数は←左の式のように与えられる。
|
|
これに対し、ガンがいくつかの質点を有し、
それぞれがバネで結合されるものと考えると、
その振動数は必ずしも↑上の式と一致しない。
またその質点の数に応じて発生しうるモードも限定されてしまう。
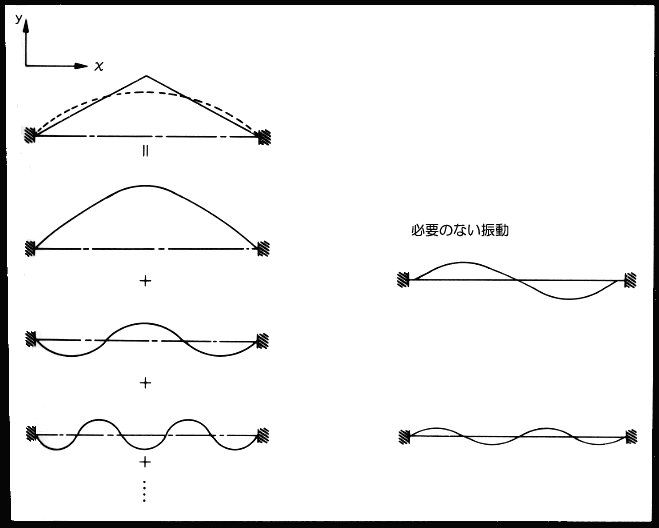
上の図↑を見ると、質点の数が多いほど
その振動の形は弦そのものに近づいてゆくことがわかる。
実際に、この質点の数が無限に多くなれば、
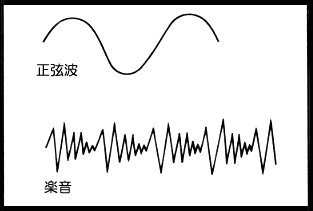
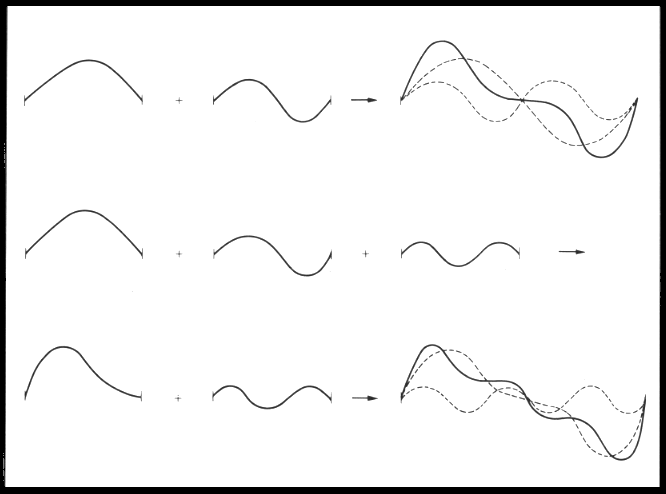
それは連続体と見なし、弦そのものと考える事ができる。 このように弦の振動は、多くの振動子が結合している 連成振動と考える事ができ、 その結果弦の振動には
(n = 1,2,3,･･･)
に与えられたように多くの成分が含まれる。
即ち多数の高調波成分が存在し、
それらが弦楽器の音色を構成しているのである。一つの振動数のみを有する音は一般に純音、正弦波と呼ばれる。 →右の図に示した波形は複雑であるが周期がある。 このような周期的な波は多くのsin波、cos波に分解されるが、 これが一般にフーリエ級数と言われるものである。 つまり逆に言うならば右の図→の波形は簡単な正弦波を 組み合わせる事によって作られている事である。 |
|
|
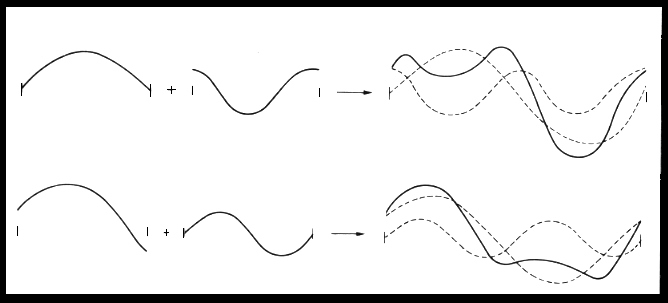
| 上の図↑を見ると、2つまたは3つ以上の正弦波を加えると 波形は異なっている事がわかる。 加え合わせる波が常に周期的であれば、 結果として生じる波も明らかに周期的であるし、 もし加え合わせる波が異なったとすると合成された波は↓下の図のように明らかに違う。 |
|
|
このようにいかなる複雑な波でも正弦波の振幅、
位相を変化させて加え合わせられていると言える。
ギターに関してこれらの考えを最も応用しているのは、
ハーモニックス(高調波)を用いた弦の調弦である。
フーリエ級数とは言えないが2つの波を合成し、
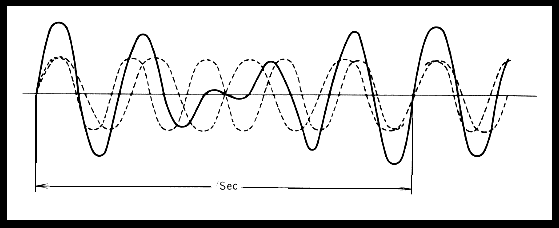
そのうなりを消すように調整しているはずである。 下の図↓のように周波数の異なる2つの波が 加え合わせられると唸(ビート)を生じる。 これは2つの周波数の差に等しいだけのビートが 1秒間に現われるのであって、下の図↓の2つの周波数を 4Hzと5Hzとすれば1秒間に1回の唸が現われる。 |
|
| ↑へ。 |
|
それではギターやその他の弦楽器の音色を決定付けている
弦振動の各高調波の成分の大きさはどのようなものであろうか。
それらは弦のどこをはじくかによって決定する。
また、ピックアップで弦振動を拾う場合には、
弦のどこにピックアップを持ってゆくかによっても異なる。
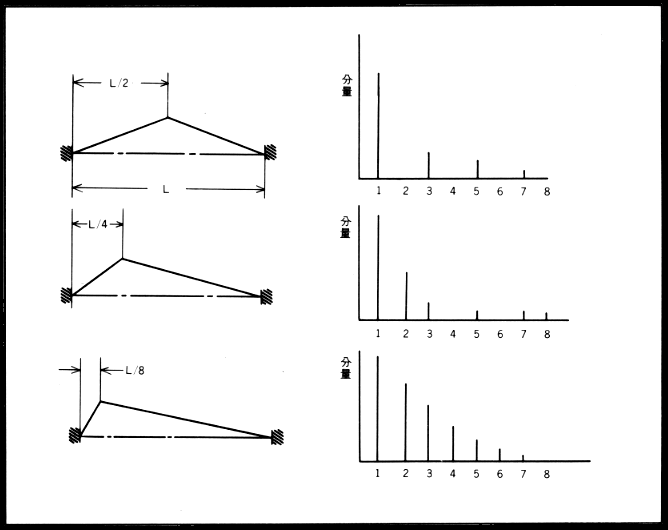
また時間が経過するとその成分の大きさの比率にも変化が現われる。 たとえば、支持点であるブリッジ近くを弾けば固い音が出るし、 また弦の中央付近を弾くと柔らかい音がする。 電気ギターには2つ以上のピックアップが取り付けられているものが多いが、 それらをスイッチで切り換えてみると、その音色の違いは明白である。 さらに弾いた瞬間と、ある程度時間が経過したあとの音色の違いも、 音量とは別に聞き取れる。 このような違いは、それぞれにおいて音を構成している各高調波の種類、 大きさにより決定されている。 ↓下の図に示したのは、弦のどこかを引張ったかによって、 その各モードの成分の相対比を見せたものである。 |
|
|
L/2に対しては2の倍数、即ち偶数次の高調波は存在せず、
同様にL/4に対しては4の倍数の高調波が存在していない。
これはL/8に対しても同じであり、他の位置に関しても全く同じように考える事ができる。
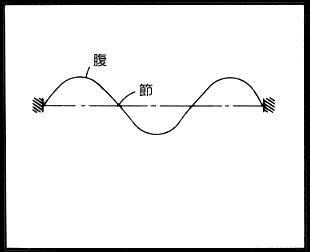
右の図→のように各モードで、振動しない部分を節(ノード)、 振幅の最も大きい点を腹(ループ)と言うが、上記のような現象はそれぞれ、 動くはずのないノードを引張ったために、 それに対応する高調波が現われないと考えることができる。 さらに引張った位置により、各高調波の成分が違うのは 引張った時の弦の最初の形によるものである。 |
|
|
| 即ち上の図↑のようにL/2を引張った場合その形は、 奇数次の高調波により形造られる。 つまりここでは中心について対称であり、 中心について対称でない偶数次の高調波は現われない。 これらの事を数式で表わすと下のように与えられる。 |
|
|
ここでyは変位量、χは弦の位置、cは弦上の波の伝播速度、
tは時間、nは各モードの番号であり、Bn、Cnはそれぞれの定数である。
最初弦を引張り、変位だけ与えないとすると、係数Cnのつく項は0となる。 狽ﾌ記号は、各nの値に対してそれぞれを加え合わせる意味を持ち、 結局↑上の式は多くの正弦波を加え合わせる事を表わす。 弦の振動は、ある時間が経過すると全く元の形に戻る。 その時間は結局、固有振動数に依存し、その振動数の逆数が周期Tであり、 元の形に帰るまでの時間である。 |
|
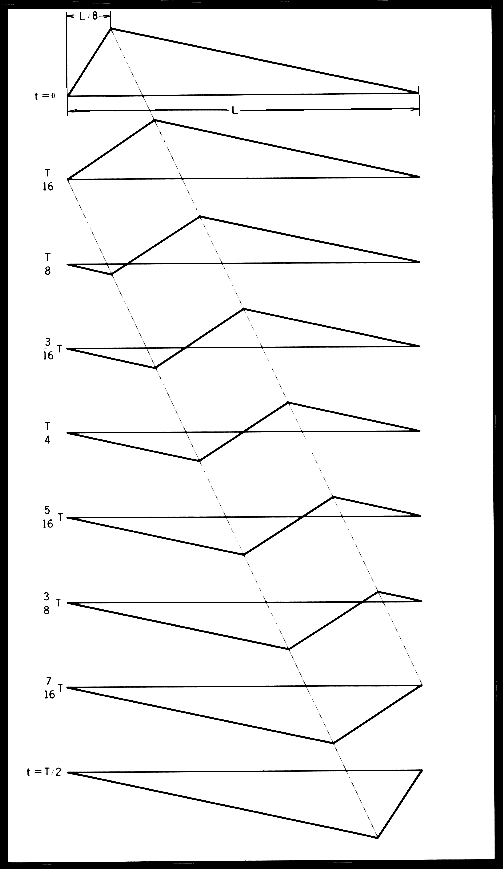
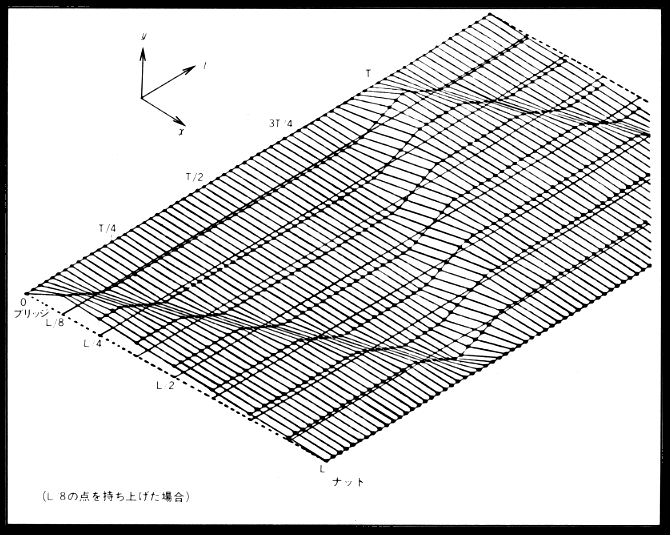
 即ち↑上の式のように表わされる。 例えばL/8の位置を引張り、はなした場合の経過は左の図←のように通りである。 この図では半周期分をT/16ごとに記しているが、 全体としてわかいやすく示したのが下の図↓である。 このように弦の振動は最初の形を、一定の周期をもって繰り返す。 一般の水の波紋や、音波などの波は、障害物となる何かが存在するならば必ず進行波と、 それと反対方向に進む反射波が存在する。弦振動もまたそうである。 両端の固定された弦ではその固定点でそれぞれの波が反射し、 両固定点の内部で2つの波が合成されたものが存在する。 下の図↓はそれらの関係を示している。 2つの波は互いに2L/Tの速度で逆向きに進む。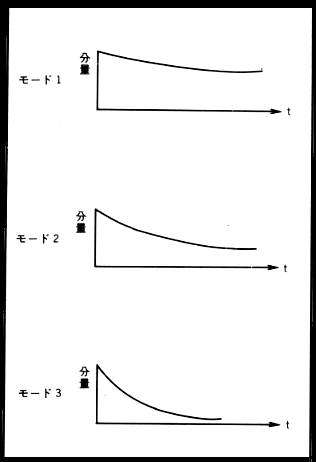 
このような弦振動の波は弦の形を変化させるだけで、
見かけ上進行していないようにも感じられるが、このような波を定在波という。
弦振動は、多くのモードの合成であり、また2つの固定点内部における定在波である事、
そしてそれらは最初の形を繰り返すものである事が以上より理解できる。しかしこのままではいつまでもその振動が継続する事になってしまう。 弦振動もまた単振動のところで述べたように減衰振動である事を考えなければならない。 さらにまた、多くの合成された各モードの振動成分が、 すべて同じ割合で減衰してゆくとは限らないのである。 実際には、↑上の図のごとく高いモード程その減衰時間は短い。 この事は前述したように、時間が経過するにつれて、 振動成分の含有量が異なってくることを表わし、 最後まで存在するのは基本モードのみである事を示している。 |
|
●弦の境界条件(ブリッジ)
| 今まで述べてきた弦の振動は、あくまで弦の両端が 完全に固定されているものという条件に基づいてきた。 2端に引張られ弦が横振動を繰り返すときは、同時に弦は伸び縮みを行っている。 即ち弦は縦振動が存在するわけであり、一般のアコースティック・ギターでは この振動がブリッジを介し表面板に伝わる。 この振動の伝わり方はブリッジや表面板の材質に大きく依存する。 アコースティック・ギターでは、弦の振動により表面板と共鳴胴が直接に 音を発するわけで、ブリッジや胴の材質に厳密な選定を必要とする。 また電気ギターは、弦の振動を電磁的に拾うわけで、 弦の両端の固定条件に関しては、さほど影響がないように思われがちである。 前述のように弦振動は定在波であり、それは進行波と、反射波が重なり合ってできている。 弦の両端が完全に固定されていれば、その境界において弦上の波は 完全に反射を繰り返し、常に同じ周期の波形を繰り返す。 しかし境界が完全に強固でないとすれば、反射波の波形は変化し、 その結果2つの波の合成波形は異なってくる。 即ちピックアップに生じる磁束変化、その結果としての電気信号は、 弦の両端の固定条件、結局ブリッジ、胴の材質により多大な影響を受ける。 結局電気ギターにおいても構造をなす各部分の材質は、 音色に大きな影響を与えているわけである。 |