振動(又は単振動)
●振動
|
振動を物理的に定義するならば、物体が一点を中心としてその前後、
または左右への運動を繰り返すことである。 振動と言える現象は、現実に多く存在するが、 単振り子(例えば柱時計の振り子)、ばね振り子など のおもりの運動は最も単純な振動の典型的なものである。 また物体の運動や変形に限らず任意の物理的な量が 一定の値を境として増減を繰り返すような場合でも振動と言う。 たとえばコンデンサーとコイルが直列につながれている 電気回路を下の図に示すが、コンデンサーに充電後 スイッチを閉じると回路に流れる電流は 規則的な変化を繰り返す。 |

|
|
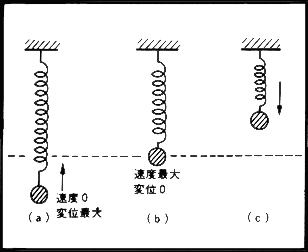
今ばね振り子のおもりを左下の図(a)の
ようにいくらか引張ったものとする。
おもりは変位しパネの弾性により元に戻る力を受ける。
おもりをはなすと動き出し 元の位置、即ち(b)の状態にきた時、
ばねはおもりに対し何の作用もしない。
そしてその時の速度は最大になる。
それは、もとの位置に戻るまで、
おもりはばねに引張り続けられるからである。
この位置を過ぎると、ばねは逆に縮み、
おもりを押し戻そうとする。 物体が振動する時、そこには変位、速度、 加速度というものが存在する。 即ちaの位置において変位を正とすれば、 変位は最大であり、速度は0、加速度は逆向きに最大である。 |
|

|
|
ばね振り子の変位、速度、加速度の関係を、
時間tに対して示すと右上の図のようになる。
このようにaの状態では、変位が最大であるが速度は0である。
またbの状態では変位が0であり、速度が最大である。 この事は前者では、位置エネルギーが最大であり、 運動エネルギーが0であるということで、 後者ではこの逆であるといえる。 このように振動は、2種類のエネルギー量の 変換を繰り返すものである。 このことは一番上の図におけるほかの 振動素子に関しても考えられる。 振動にはまず何らかの原因が必要である。 即ち、ばね振り子に対しては、引張ってやるか又は、 縮ませてやるかの力を加える必要がある。 こうして、ばね振り子は振動を始めるが、 その運動が単位時間に繰り返される回数を、振動数と呼ぶ。 今、単位長だけの変位を生じる時の、 ばねの引張る力、または押し戻そうとする力をk、 おもりの質量をmとすると、振動数はνは次のように表わされる。 |
|
|
|
これは2階線形常微分方程式を解いた結果として得られる。
上の式の振動数でおもりは振動を始めるが、
振動は実際に小さくなっていく。
エネルギーは、物体に対して仕事をする能力を持っている。
即ちエネルギーの量が不変な限り振動は持続する。
しかし実際の振動では、摩擦などの抵抗力により、
エネルギーが熱になりその分、振動を減じさせてしまう。
その結果、時間がたつと振動は止まる。 このような振動を減衰振動と呼び、現実に存在する すべての振動がそうである。 減衰を供なう原因となる要素は、複雑であるが、 一般的に速度に比例する抵抗力を示すような 定係数となるものについては、比較的簡単に解く事ができる。 このような場合振動数は上の式の場合と若干異なる。 また振動数の逆数は、1回だけ振動を行うのに必要な時間で、 周期と呼ばれるが、減衰振動の場合、抵抗のない場合と 比較して長くなる。 下の図に減衰振動を示す。その振幅の減少は、 抵抗の成分によって決定つけられる。 ギターにおける弦振動も減衰振動である。 |

|
|
ここまで一つのばねとおもりを有する振動系に関して述べてきた。
そしてそれらは任意の条件を与えて、
自由に振動させるものであった。
そういう意味において、ギターの弦もピッキング、
あるいは手で弾く事により条件を与えるとすれば同一のものである。
振動体の振動数は上の式で表わされる事を述べたが、
これは固有振動数とも呼ばれる。
この固有振動数と、強制力の振動数が一致したときに、
振幅が著しく増大するというのが共振現象である。 もし、摩擦などの抵抗がまったくないものとすれば、 共振振動数において振幅は無限に大きくなる。 上の図に減衰振動と強制振動の関係を示す。 このように過渡成分である減衰振動は、 時間の経過に伴ない消滅してしまうが、 それは抵抗が大であればそれだけ速やかに減衰してしまう。 |

|
| 上の図に振動系の固有振動数と、強制力の振動数との 比に対する振動の関係を、抵抗rの大小に応じて示す。 ここで、λ= r/2m、ωο= 2π×νο、ω=2π×ν、 h=λ/ωという関係にある。 現実には何らかの抵抗が存在し、また振動系の構造上の制限もあり、 共振時に振幅が無限に大きくなることはありえない。 強制力が連続して仕事をする以上、 損失がなければ振幅は増大してゆくが、 必ず失われるエネルギーも存在する。 これらの共振の鋭さは、Q値(quality factor-value)、 または半値幅と呼ばれるもので定義される。 Qは貯えられるエネルギーと、消費されるエネルギーとの比であり 次のように定義される。 |
|
|
| また下の図に示すような共振曲線のピーク値の1/√2に 等しくなる振動の差を半幅値と呼び、 これを用いても共振の鋭さを表わす事もでき 右下のように定義される。 |

|
|
| 上の2つの式はまったく同一の関係である。 以上のように、一つのばねと重りによる振動系は 一つの振動数において共振を生じる。 このような振動系を単一共振系と呼び、 自由度が1であるともいう。 多くの振動系は、このように簡単ではないが、 単一共振系が複雑に組み合わされたものであると 考える事ができる。 |
| ↑へ。 |
| Academic Zone >基礎知識 >振動 |